Понимание роли математических методов в финансовых стратегиях может значительно улучшить процессы принятия решений в области финансового менеджмента. Будь то инвестиционный анализ, управление рисками или даже прогнозирование рынка, использование математических инструментов играет центральную роль в точной оценке переменных и тенденций. С помощью алгоритмов математические модели помогают специалистам выявлять закономерности, рассчитывать вероятности и прогнозировать результаты, что крайне важно для оптимизации бизнес-стратегий.
Численные методы и модели служат основой различных процессов, таких как определение процентных ставок, управление денежными потоками и даже оценка финансовых деривативов. Эти методы используются во многих отраслях, обеспечивая стабильность и рост организаций, а также позволяя понять, как корректировка финансовых стратегий может повлиять на общие показатели. Использование сложных математических моделей позволяет более эффективно распределять ресурсы, минимизировать возможные потери и максимизировать прибыльность.
В частности, в области банковских операций внедрение математических моделей позволяет более точно анализировать кредитный риск, стоимость активов и стратегии управления капиталом. Способность предсказывать финансовые кризисы или колебания рынка с помощью этих моделей незаменима для учреждений, работающих с большими объемами данных и сложными финансовыми инструментами. Сосредоточившись на математических принципах, управляющих экономическим поведением, профессионалы в этой области лучше подготовлены к прогнозированию изменений на рынке, принятию политических решений и консультированию клиентов.
Количественные модели для экономического прогнозирования
Для точного прогнозирования будущих тенденций в финансовом секторе неотъемлемую роль играют количественные модели. Эти модели опираются на математические инструменты для анализа исторических данных и составления прогнозов, которые могут служить основой для принятия решений. Применяясь в контексте финансовых систем, они предлагают бесценные знания в области управления рисками, ценообразования активов и общей стабильности рынков.
- Регрессионный анализ часто используется для понимания взаимосвязи между различными переменными. Например, он помогает определить, как определенные рыночные показатели, такие как процентные ставки или инфляция, влияют на экономические показатели.
- Анализ временных рядов позволяет исследовать прошлые точки данных за регулярные промежутки времени, помогая предсказать будущие движения на основе исторических закономерностей.
- Моделирование методом Монте-Карло используется для моделирования вероятности различных исходов в процессе, который невозможно легко предсказать из-за вмешательства случайных переменных. Этот метод очень эффективен при прогнозировании волатильности рынка и рисков.
Применение этих методов в финансовой сфере помогает менеджерам и аналитикам разрабатывать более обоснованные стратегии. Например, при рассмотрении стратегий управления активами или ценообразования регрессионные модели дают четкое представление о том, как различные факторы, такие как изменения в политике, влияют на доходность. Модели временных рядов еще больше уточняют эти прогнозы, оценивая прошлые данные для прогнозирования будущих событий.
В банковском секторе количественные модели помогают в стресс-тестировании, оценке кредитного риска и потенциальных рыночных потрясений. Внедряя эти подходы в управление рисками, финансовые учреждения могут лучше ориентироваться в условиях неопределенности и оптимизировать свою деятельность.
Эти математические инструменты, несмотря на их сложность, предназначены не только для опытных практиков. При соответствующей подготовке они могут эффективно применяться такими профессионалами, как финансовые аналитики, политики и научные исследователи. Глубокое понимание этих методов позволяет разрабатывать более точные прогнозы, что в конечном итоге способствует повышению стабильности финансовых рынков и обоснованному экономическому планированию.
Методы управления рисками в банковской сфере

1. Оценка кредитного риска: Для эффективного снижения рисков банки должны опираться на модели, предсказывающие вероятность дефолта заемщика. Применение сложных алгоритмов позволяет лучше понять особенности финансового поведения, что дает возможность учреждениям оценить потенциальные убытки и установить соответствующие требования к залогу. На практике это предполагает анализ финансовой отчетности, исторических данных и профилей клиентов для создания надежной матрицы рисков.
2. Управление рисками, связанными с процентными ставками: Финансовые учреждения часто сталкиваются с проблемой колебания процентных ставок. Используя производные финансовые инструменты, такие как свопы и опционы, банки могут стабилизировать доходность кредитов с фиксированной процентной ставкой и избежать потерь в связи с изменениями на рынке. Эта стратегия помогает снизить влияние непредсказуемых экономических изменений на их балансы.
3. Контроль риска ликвидности: Управление ликвидностью жизненно важно для поддержания операционной стабильности банка. Стратегии управления ликвидностью предполагают постоянный мониторинг денежных потоков и обеспечение достаточных резервов для удовлетворения потребностей в снятии средств. Банки часто используют модели стресс-тестирования для моделирования экстремальных сценариев, оценивая свою способность справиться с внезапными экономическими потрясениями.
4. Снижение операционного риска: Мошенничество, сбои в работе систем и внутренние ошибки — все это операционные риски, которые могут угрожать стабильности банка. Чтобы минимизировать эти риски, многие учреждения используют системы мониторинга в режиме реального времени и проверки соблюдения требований. Внедрение надежной системы внутреннего аудита гарантирует, что потенциальные проблемы будут обнаружены на ранней стадии и оперативно решены.
5. Хеджирование рыночных рисков: Банки также подвержены рыночным рискам, таким как колебания цен на активы или валютных курсов. Стратегическое использование инструментов хеджирования, включая фьючерсные и форвардные контракты, позволяет учреждениям ограничить подверженность неблагоприятным изменениям на рынке. Прогнозируя возможные рыночные тенденции и соответствующим образом корректируя портфели, банки могут защитить свои активы от непредвиденных событий.
6. Соблюдение нормативных требований: Соблюдение требований местных и международных нормативных актов является ключевым фактором для обеспечения надежной системы управления рисками. Чтобы избежать штрафов и защитить свою репутацию, банки должны проводить строгие проверки на соответствие нормативным требованиям. Это включает в себя постоянное изучение финансовых законов и их учет в ежедневной практике управления рисками.
7. Диверсификация рисков: Диверсифицированный портфель — один из наиболее эффективных методов распределения рисков по нескольким направлениям. Держа в портфеле различные финансовые инструменты, такие как акции, облигации и недвижимость, банки могут снизить риск, связанный с каким-либо одним классом активов. Такая стратегия снижает общий риск финансовых потерь и обеспечивает большую долгосрочную стабильность.
Алгоритмы оптимизации для управления портфелем
Чтобы максимизировать доходность при минимизации риска при управлении портфелем, необходимо использовать методы оптимизации, которые позволяют динамично корректировать распределение активов. Одним из таких методов является применение алгоритмов линейного программирования, которые позволяют портфельным менеджерам распределять активы на основе исторических данных и ожидаемой доходности. Эти алгоритмы позволяют менеджерам сбалансировать риск и доходность, используя такие ограничения, как лимиты капитала, ограничения на активы и требования к диверсификации.
С практической точки зрения эти алгоритмы принимают решения на основе заранее определенной целевой функции, обычно максимизирующей ожидаемую доходность при заданном уровне риска. Например, управляющий портфелем может применить модель оптимизации средней дисперсии Марковица, которая рассчитывает оптимальное сочетание активов на основе ожидаемой доходности и ковариации между доходностями активов. Однако этот метод может иметь ограничения, когда речь идет о реальных ограничениях, таких как транзакционные издержки или соображения ликвидности.
Еще один передовой подход — использование генетических алгоритмов, которые имитируют процесс естественного отбора для создания лучших конфигураций портфеля. Эти алгоритмы используют методы случайной мутации и кроссинговера для изучения более широкого диапазона возможных распределений портфеля, что часто приводит к лучшим результатам, чем традиционные модели. В ситуациях, когда данные неполны или зашумлены, генетические алгоритмы обеспечивают надежный метод для изучения различных сценариев и оптимизации структуры активов.
Интеграция алгоритмов оптимизации в управление портфелем также распространяется на стратегии управления рисками. Например, модели Value at Risk (VaR) в сочетании с методами оптимизации позволяют менеджерам оценивать потенциальные потери в различных рыночных условиях, что дает возможность принимать обоснованные решения о хеджировании и выборе активов. Применяя эти алгоритмы, портфельные менеджеры могут не только обеспечить высокую доходность, но и защитить портфель от значительных спадов.
Кроме того, эти методы позволяют систематически оценивать компромиссы между риском и доходностью. Например, сценарный анализ, реализуемый с помощью алгоритмов оптимизации, позволяет управляющим портфелями оценить потенциальное влияние рыночных потрясений или изменений экономических условий. Такой уровень анализа гарантирует, что решения будут основываться на количественных данных, а не на субъективных суждениях.
В заключение следует отметить, что использование алгоритмов оптимизации в управлении портфелем является сложным и мощным инструментом управления инвестиционными рисками. Используя эти модели, профессионалы в данной области могут принимать решения, основанные на данных, которые соответствуют как краткосрочным, так и долгосрочным финансовым целям, что свидетельствует о значительной роли математических инструментов в современных инвестиционных стратегиях.
Математика, лежащая в основе расчетов по кредитам и ипотеке
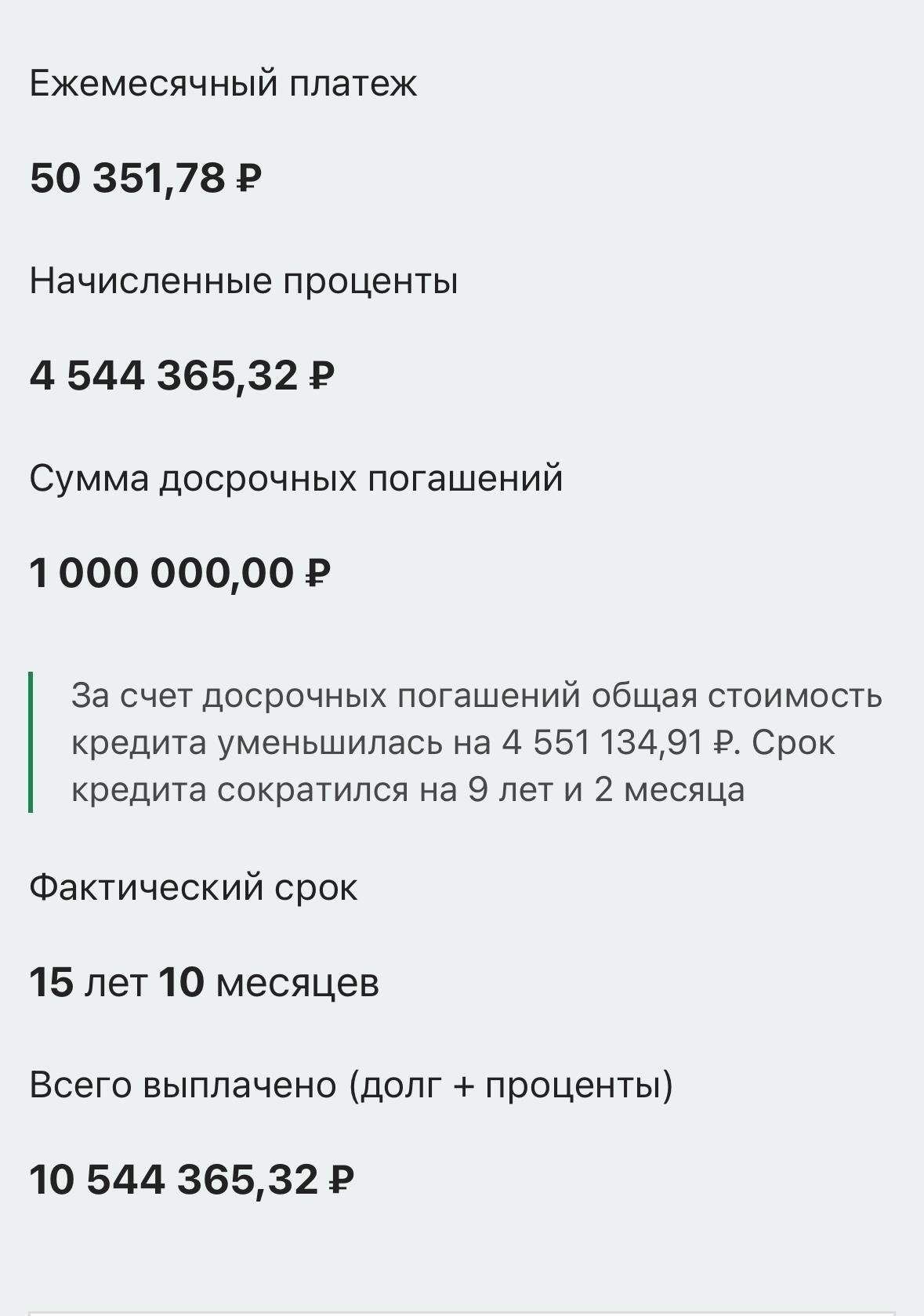
Чтобы точно рассчитать платежи по кредиту или ипотеке, необходимо применить специальные математические формулы, учитывающие основную сумму долга, процентную ставку и время. В финансовом секторе эти расчеты обеспечивают понимание кредиторами и заемщиками условий погашения кредита. Типичная формула, используемая для расчета ежемесячных платежей, основана на процессе амортизации, который делит кредит на равные платежи в течение определенного периода.
В случае ипотечного кредита формула ежемесячного платежа выглядит следующим образом:
- Ежемесячный платеж = P [ r(1+r) n ] / [ (1+r) n — 1 ]
Где P — сумма основного долга, r — ежемесячная процентная ставка (годовая процентная ставка, деленная на 12), а n — количество платежей (срок кредита в месяцах). Эта формула обеспечивает постоянство платежей, в то время как доля основной суммы и процентов меняется с каждым платежом.
Математические модели также важны при определении остатка по кредиту после определенного количества платежей. Формула для такого расчета выглядит следующим образом:
- Остаток по кредиту = P [(1+r) n — (1+r) t] / [(1+r) n — 1].
В этом уравнении t означает количество уже сделанных платежей. Этот расчет крайне важен для рефинансирования или понимания того, какую сумму придется выплатить через определенный период. Финансовые учреждения используют эти модели для прогнозирования будущих денежных потоков, оценки рисков и определения подходящих условий кредитования для клиентов.
Для заемщиков понимание этих формул — ключ к тому, чтобы выплаты по кредиту были приемлемыми. При правильном применении эти формулы могут помочь определить оптимальный график платежей, минимизировать процентные выплаты и избежать потенциальных финансовых трудностей.
Математика в ценообразовании финансовых деривативов
При ценообразовании финансовых деривативов крайне важно применять передовые методы количественного анализа. Один из наиболее распространенных методов предполагает использование стохастических процессов, таких как броуновское движение, для моделирования колебаний цен активов. Эта модель очень важна для определения стоимости деривативов, поскольку она позволяет реалистично моделировать рыночные условия с течением времени.
Стохастические дифференциальные уравнения в ценообразовании
Чтобы понять процесс ценообразования, мы можем рассмотреть модель Блэка-Шоулза, которая использует стохастические дифференциальные уравнения (SDE) для определения справедливой цены опционов. SDE описывают эволюцию цен на активы, учитывая случайность и волатильность, наблюдаемые на реальных рынках. Решив эти уравнения, аналитики могут рассчитать цену опциона с поправкой на такие факторы, как время до погашения, безрисковая процентная ставка и волатильность.
Роль риск-нейтральной оценки
Еще одним важным математическим инструментом, используемым в ценообразовании деривативов, является концепция нейтральной оценки риска. В рамках этой концепции все будущие денежные потоки дисконтируются по безрисковой ставке, предполагая, что инвесторы безразличны к риску. Этот подход упрощает оценку деривативов, устраняя необходимость моделирования предпочтений в отношении риска и фокусируясь исключительно на ожидаемом движении цены базового актива.
Применение теории игр в банковских стратегиях
Применение теории игр в процессе принятия финансовых решений значительно повышает способность банков разрабатывать конкурентные стратегии. Этот подход опирается на математические модели для анализа стратегических взаимодействий, что позволяет учреждениям принимать обоснованные решения в условиях жесткой конкуренции. Ниже приведены ключевые приложения:
- Стратегии ценообразования: Банки могут использовать теорию игр для прогнозирования реакции конкурентов на изменение процентных ставок или платы за услуги. Это поможет установить конкурентоспособные, но выгодные цены, не провоцируя ценовых войн.
- Решения о входе на рынок и выходе из него: Теория игр помогает банкам оценить оптимальное время для входа или выхода на рынок, основываясь на действиях существующих конкурентов и потенциальных изменениях на рынке.
- Управление кредитными рисками: С помощью теоретико-игровых моделей банки могут анализировать поведение заемщиков и конкурентов с точки зрения кредитного риска, что способствует разработке более надежных критериев кредитования.
- Переговоры и стратегические альянсы: При ведении переговоров с другими финансовыми организациями применение теории игр позволяет банкам прогнозировать действия конкурентов и противодействовать им, улучшая результаты переговоров.
Использование математических инструментов в этих областях позволяет получить ценные сведения о поведении клиентов, стратегии конкурентов и динамике рынка. Это способствует более обоснованному подходу к управлению рисками и принятию решений в финансовом секторе.
Математические методы в моделях кредитного скоринга
Использование передовых количественных методов имеет решающее значение для оценки кредитоспособности физических и юридических лиц. Применение статистических моделей и алгоритмов прогнозирования помогает определить вероятность погашения кредита на основе различных факторов, таких как доход, долг и кредитная история.
Как правило, эти модели включают в себя такие методы, как регрессионный анализ, деревья решений и логистическая регрессия. Эти инструменты позволяют финансовым учреждениям оценивать уровень риска и принимать решения на основе данных. Ключ к их эффективности заключается в способности обрабатывать большие объемы данных и предоставлять практические выводы.
Комбинируя эти методы, финансовое учреждение может создать модель, которая с высокой точностью оценивает профиль риска заявителя. Практическое применение этих методов позволяет создавать более надежные и прочные системы кредитного скоринга.
Анализ данных для разработки экономической политики
Для выработки разумной экономической политики крайне важен строгий подход к анализу данных. Применение математических моделей обеспечивает конкретную основу для понимания последствий политических решений. Используя передовые статистические методы, аналитики могут тщательно проанализировать огромный массив экономических данных и получить четкое представление о возможных результатах.
Многие политические решения принимаются с помощью моделей, основанных на данных, которые необходимы для доказательства влияния различных вариантов политики. Например, математические инструменты позволяют анализировать тенденции занятости, уровень инфляции и распределение доходов, обеспечивая точное представление о долгосрочных последствиях предлагаемых изменений.
Математический анализ ситуации позволяет выявить ключевые переменные, влияющие на экономику. Благодаря такому структурированному анализу становится возможным прогнозировать последствия тех или иных политических мер, предлагая законодателям руководство для принятия взвешенных решений. Эти модели широко используются в различных областях, демонстрируя их широкую применимость в реальных сценариях.
На практике политики полагаются на документы, в которых сведены воедино математические доказательства и симуляции, полученные на основе данных. Например, документы с подробным описанием эконометрического анализа часто становятся основой для официальных политических рекомендаций. Поэтому анализ таких документов играет важную роль в оценке жизнеспособности предлагаемой политики, обеспечивая принятие решений на основе количественных данных.
Применение сложных моделей данных в экономической политике гарантирует, что предлагаемые меры не только теоретически обоснованы, но и подкреплены эмпирическими данными. Такой подход доказывает, что обоснованные экономические решения опираются на данные, а не на домыслы или непроверенные предположения.